Monty Hall Problem Simulator

A Monty Hall problémája a valószínűségi elmélet egyik leghíresebb matematikai problémája:

Egy televíziós játékban a fogadó megkéri a játékosokat, hogy válasszanak ki egyet a három zárt ajtó közül, amelyek a lejátszó előtt vannak. A két ajtó mögött kecske és az egyik ajtó mögött egy autó, amelyet a játékos nyerhet, amikor az ajtót választja. Miután a játékos kiválasztotta az egyik ajtót (amely továbbra is zárva van), a házigazda kinyit egy másik ajtót, amely mögött kecske van. A fogadó megkérdezi a játékostól, hogy az elején kiválasztott ajtón akarja-e maradni, vagy a másik zárt ajtóra szeretne váltani.

A kérdés nyilvánvalóan: ha a játékos átkapcsolja az ajtót vagy a kiválasztott ajtón marad?

Sokan azt mondhatják, hogy nem számít, hogy a játékos átkapcsolja-e az ajtót, vagy sem, mert az autó nyerésének valószínűsége 50/50. Bár ez úgy tűnik ésszerűnek, mert két azonos zárt ajtó van, ez a rossz válasz.

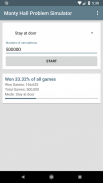
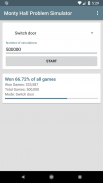
A helyes válasz az, hogy az autó megszerzésének esélye 67%, ha a játékos az ajtót váltja, és csak 33% -ot, amikor a játékos az első ajtónál marad.

Nem hisz el találkozni? Töltse le az alkalmazást, és próbálja ki!

Ez az alkalmazás lehetővé teszi, hogy automatikusan le tudja szimulálni a leírt játékot, akár 5 millió alkalommal egymás után. Kiválaszthatja, hogy a szimulált játékos mindig kapcsolja-e az ajtót vagy mindig az általa választott ajtón maradjon. Miután az alkalmazás szimulálta a kért számú játékot, megad egy statisztikát, amely megmutatja, hogy hány játékot nyert a játékos. Így meg tudja tudni, hogy a játékosnak be kell-e kapcsolnia az ajtót.